本讲我们来探讨动态规划算法中一个常见的问题最长公共子序列即LCS(Long Common Sequence)。

首先我们来看一下问题描述：

有两个序列X和Y，其中

X = {x1, x2, ..., xm}

Y = {y1, y2, ..., yn}

求X和Y的最长公共子序列长度。

例如：X={1, 3, 5, 9, 10}  Y={1, 4, 9, 10}，则X和Y的最长公共子序列的长度为3，其中一个序列为{1，9，10}。

解题思路：

步骤1：用函数的形式来表示结果。

设f(x,y) = z，该函数表示X序列的长度为x, Y序列的长度为y，则XY序列的最长公共子序列长度为z。

所以题目要求解的便是f(m,n)的值。

步骤2：分析递推情况。

接下来我们来分析一般情况即f(i,j)的求解。

f(i,j)表示有两个序列

X = x1, x2, ..., xi

Y = y1, y2, ..., yj

如何求这两个子序列的最长公共子序列的长度。

所谓的递推关系分析其实就是分析f(i)与f(i-1)、f(i-2)...或f(0)等之间的关系，由于本题是二元函数关系，故就是分析f(i,j)与f(i-1,j-1)、f(i-1,j)、 f(i, j-1)等之间的关系。

首先我们来看一下f(i,j)与f(i-1, j-1)之间的关系。

f(i,j)表示的是规模分别为i和j的两个序列的最长公共子序列的长度，而f(i-1, j-1)表示的是规模分别为i-1和j-1的两个子序列的最长公共子序列的长度。

这两者之间有什么联系呢？

假设我们现在已经知道f(i-1, j-1)的最长公共子序列的长度，现在要求f(i,j)函数的值，你该如何求解？

当两个序列的最后一个元素相等时，此时f(i,j)的值应该就是f(i-1, j-1) 的值加上1，即

f(i,j) = f(i-1, j-1) + 1， 这种情况比较好理解。

当两个序列的最后一个元素不等时，则我们需要考虑f(i-1, j)和f(i, j-1)的最大值，即max{f(i-1, j), f(i, j-1)}。

综上，我们可以得出下面的递推关系式：

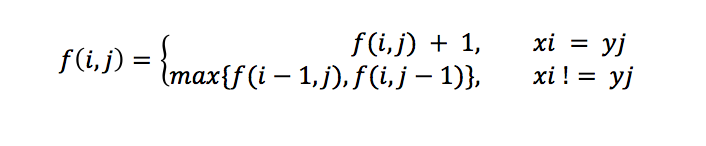
步骤3：算法实现

算法实现我们将开辟新的文章来讲解，敬请期待。

总结：

无论什么样的动态规划题目我们基本都可以按照上面的思路来求解，步骤一其实就是问题的分解，寻找合适的自变量来控制问题的规模，步骤二的递推关系分析也有一定的规律可循，后面将开辟新的文章来分析。